Don't Hash Your Secrets

Ben Adida suggests that you don't hash your secrets.

That means that if you know SHA1(secret || message), then you can compute SHA1(secret || message || ANYTHING), which is a valid signature for message || ANYTHING. So to break this system, you just need to see one signature.

Not being a cryptography expert, I was blown away by his article. At the core of his post is the idea that given a hash digest of a message, one could compute the hash of message + appended_message without even knowing the original message.

I had to see this for myself. Was it that easy to extend an MD5 or SHA1 hash? Below, you'll find working python code and an explanation for spoofing signatures signed with the MD5 algroithm.

Implementation

To generate a hash from a message, algorithms like MD5 and SHA1 iterate through the message block by block. For each block, the algorithm runs a transformation function where the input is a seed state and a message block . The output of this transformation is then fed back as the seed state for the transformation of the next message block (see the above diagram).

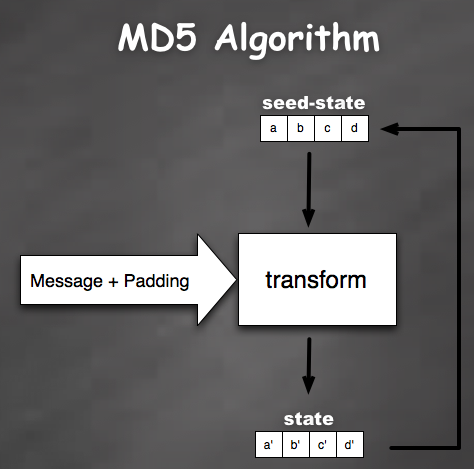
After the hashing function has digested the entire message, it then appends some padding and runs the transformation function one more time. The final state of this transformation becomes the digest.

from hashlib import md5
signature = md5("secret" + "hello world").digest()

print(repr(signature))
"O'Q\xa8\xb8\x9d\x81%\xd7\x13'\xe0\xfb_2\xde"

In the code above, the signature represents the state output of the final transformation function.

AHA! We now have a strategy to extend the hash. If we can seed the transformation function with the state(AKA signature) of the original message, we can essentially extend the hash without even knowing the original message.

There is one problem however. I mentioned before that the MD5 algorithm adds a piece of padding to the original message before it gives us the hash. That means whenever we see a signature it's really the hash of the message + padding. Fortunately, the padding is only dependent upon the length of the original message. With that in mind, we can easily generate both the new signature and padding. Here's some pseudocode

state = decode(signature)
padding = calculate_padding(original_message_len)
new_signature = transform(state, "appended message")

# This should be True
new_signature == md5(original_message + padding + "appended message").digest()

Now here is the real code.

def spoof_digest(originalDigest, originalLen, spoofMessage=""):
    # first decode digest back into state tuples
    state = Decode(originalDigest, 16)

    # generate a seed md5 object
    spoof = md5()

    # seed the count variable for calculation of index, padLen, and bits
    spoof.count += originalLen << 3

    # calculate some variables to generate the original padding
    index = int((spoof.count >> 3) & 0x3f)
    padLen = (56 - index) if index < 56 else (120 - index)
    bits = Encode((spoof.count & 0xffffffffL, spoof.count>>32), 8)

    # construct the original padding
    padding = PADDING[:padLen]

    # augment the count with the new padding and trailing bits
    spoof.count += len(padding) << 3
    spoof.count += len(bits) << 3
    spoof.state = state

    # run an update
    spoof.update(spoofMessage)

    # We now have a digest of the original secret + message + some_padding
    return (spoof.digest(), padding + bits)

The code has a dependency on a pure-python implementation of the md5 algorithm that I've packaged it together with the source code. If you want to try it out, download the file and run this test function (also included in the file):

def test_spoofing():
    originalMsg = "secret" + "my message"
    appendedMsg = "my message extension"

    # This is the signature that a legitimate user sends
    # over the wire in clear text. 
    originalSignature = md5(originalMsg).digest()

    # This is how an attacker would spoof the signature where,
    # the message ==  originalMsg + padbits + appendedMsg .
    # Notice that this method implies that the attacker
    # knows the original length of the "secret" ... 
    # Most apis such as Flickr assign secrets that are of
    # uniform length for all of their api users.
    spoofSignature, padbits = spoof_digest(originalSignature, len(originalMsg), appendedMsg)

    # This is how a legitimate user would construct the
    # a signature when message == originalMsg + padbits + appendedMsg
    testSignature = md5(originalMsg + padbits + appendedMsg).digest()

    # make sure the spoof signature and the test signature match.
    # if, this passes, we've successfully constructed a spoofed message
    # of the form: secret + orginal_message + padding + appended_message
    # without actually knowing the secret.
    assert testSignature == spoofSignature

Information in this blog is meant for educational purposes only!

Show or Add Comments

Don't Hash Your Secrets

Implementation

Discussion