When installed and linked correctly against a blas implementation like ATLAS or
OpenBlas, numpy’s dot product can run incredibly fast. What I hadn’t known until recently is that for some special cases, you can perform dot products an order of magnitude faster just by calling the underlying blas routines directly.
In order to do so, I’ve written a module called fastdot, whose source code is located in a github gist.
The code, in a nutshell, is a wrapper around blas’s generalized matrix-matrix multiplication routines (A.K.A “gemm”). Its main job is to ensure that the arrays that get passed into it are in FORTRAN contiguous order before handing-off the bulk of the work to the underlying blas routines.
Performance comparison between dot product implementations
I ran a few benchmarks and plotted below the speed differences between fastdot.dot and np.dot operating on matrices of varying dimensions and sizes.
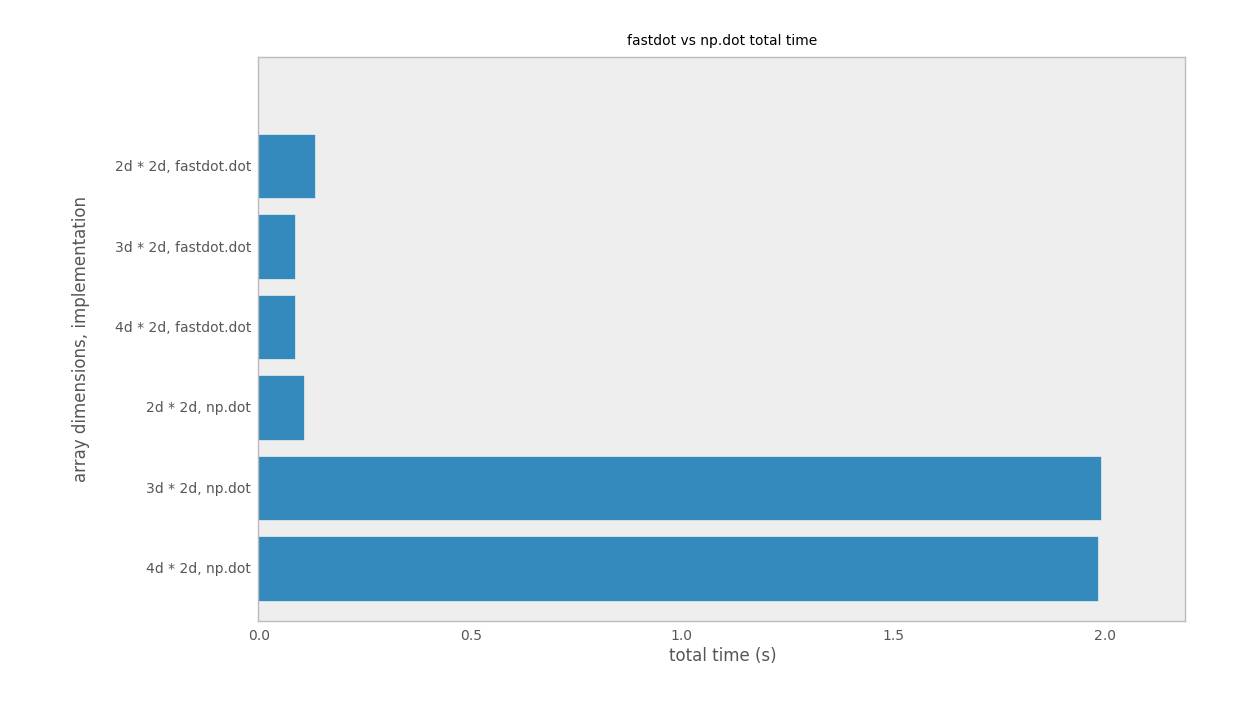
A shape B shape array dims function time (s)
----------------- ---------- ------------ ----------- ----------
(8, 55, 55, 1024) (1024, 92) 4d * 2d np.dot 2.0168
(440, 55, 1024) (1024, 92) 3d * 2d np.dot 1.9883
(24200, 1024) (1024, 92) 2d * 2d np.dot 0.0944
(8, 55, 55, 1024) (1024, 92) 4d * 2d fastdot.dot 0.1187
(440, 55, 1024) (1024, 92) 3d * 2d fastdot.dot 0.0940
(24200, 1024) (1024, 92) 2d * 2d fastdot.dot 0.1342As you can see fastdot.dot runs almost 20X faster than np.dot when one of your matrices has 3 dimensions or more. But before you start using it everywhere that you need a dot product, do take notice that it runs slightly slower than numpy’s implementation when operating on matrices with 2 dimensions or less.
As a rule of thumb, use fastdot when you know ahead of time that the number of dimensions in your matrices will be larger than 3. It could increase your program’s performace by 20x. Otherwise stick with numpy’s implementation.

Discussion