Why Uncertainty Matters in Deep Learning and How to Estimate It

More trustworthy models
Uncertainty estimates, what are they good for?
Sources of uncertainty
How to estimate uncertainty (overview)
How good are these uncertainty estimates?
Moving beyond traditional leaderboard metrics
References

More trustworthy models

For safety critical systems and infrastructure, you need to know when to trust a model’s prediction and when you should be more cautious about its output.

The problem with conventional deep neural networks is that they only provide point-estimates which are single predictive values given some input data. What you don’t get with these models is a measure of how uncertain they are for any given prediction.

While the softmax “probability” of a neural network classifier is commonly interpreted and used as a heuristic for uncertainty, scientists have shown that this measure often overestimates its confidence, even on examples that are unrecognizable when compared to a model’s training set.

What we really need is an accurate measure of uncertainty. Having one lets your model say “I don’t know” when it encounters a distribution of data that it wasn’t trained with or when it evaluates an example that can be interpreted in multiple ways.

Uncertainty estimates, what are they good for?

Accurate uncertainty estimates give you more flexibility when dealing with your model. You don’t have to always assign the same amount of trust to every model prediction, and likewise, you don’t always have to take the same action based upon those predictions.

For example, when uncertainty is high you can decide to:

Refrain from taking any action on the prediction at all.
Refer the particular piece of data to a human to make a final call.
Collect more examples that cause high uncertainty to retrain your model.
Implement a tiered prediction strategy by sending the data to a slower, but more accurate model, when uncertainty is high.

Blindly assigning the same amount of trust and action for every model prediction can lead to embarrassing, serious, or even fatal mistakes in your autonomous systems.

Sources of uncertainty

We have to understand where uncertainty comes from to know how we can account for it in our models. Let’s look at two major sources of uncertainty in predictive modeling below.

Aleatoric uncertainty is uncertainty arising from noisy data. The noise can come from observation noise or it can come from the underlying process itself. High Aleatoric uncertainty indicate that small changes in the input data lead to large variances in the target data.

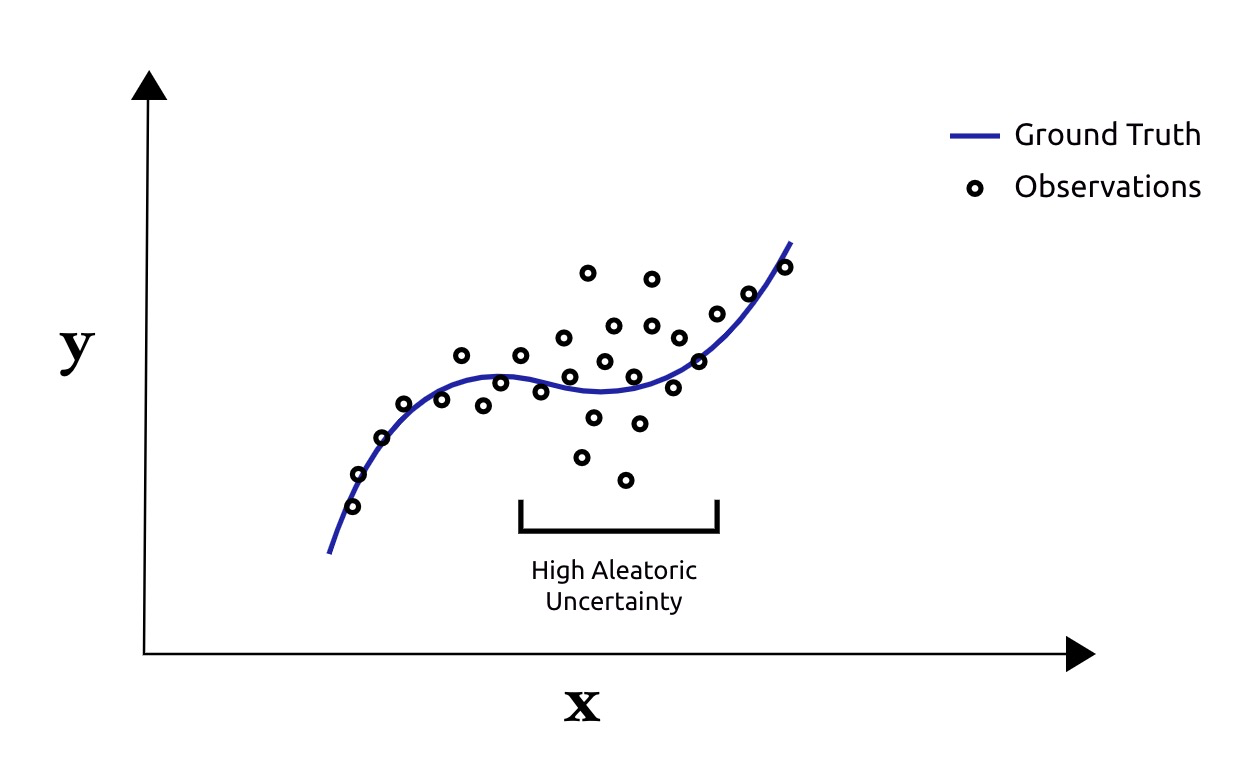
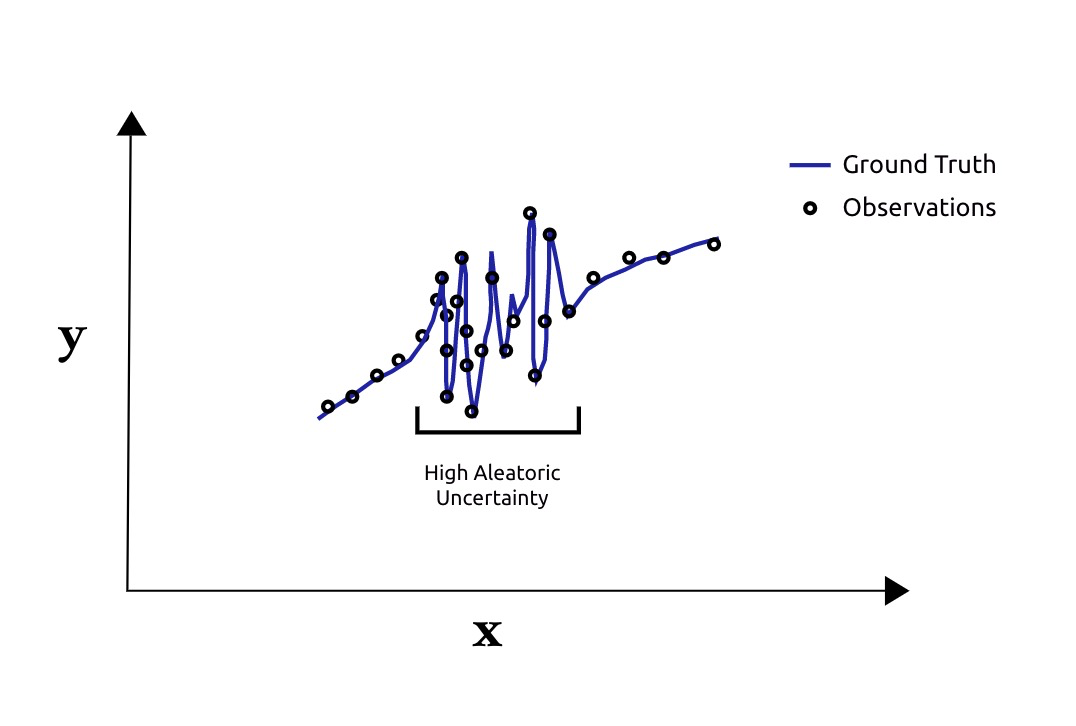
Noisy measurements of an underlying process leading to high Aleatoric uncertainty.

Even with error-less observations, a noisy underlying process can give rise to high Aleatoric uncertainty.

Epistemic uncertainty is uncertainty arising from a noisy model. Given the same input, high epistemic uncertainty indicate that small changes in model parameters give rise to large changes in model predictions. This type of uncertainty commonly occurs when models are evaluated on data whose distribution is different from the training data.

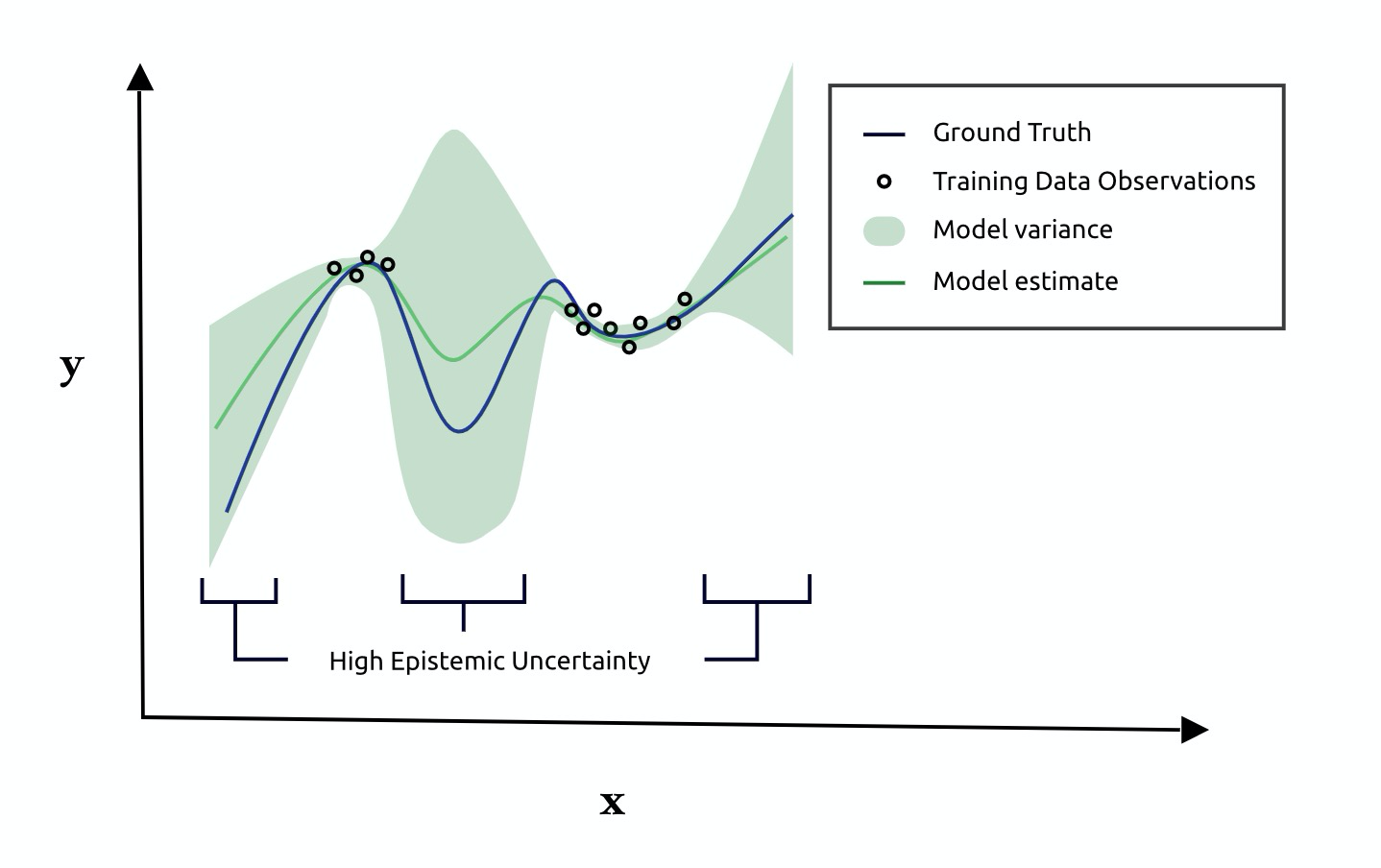
Epistemic uncertainty can arise in regions of the data space where there are few observations for training. This is because when there is little training data, many plausible model parameters may suffice for explaining the underlying ground truth phenomenon.

How to estimate uncertainty (overview)

There is ongoing research into how best to estimate uncertainty and it is not a solved problem yet. Monte Carlo Dropout and Model Ensembling are methods that have garnered recent attention because they mesh well with existing neural network architectures and are less computationally constrained than other methods.

These methods try to account for both aleatoric and epistemic uncertainty.

Although the authors behind these methods give different motivations for their work, both approach the problem of estimating uncertainty using a similar strategy:

They first propose modifying your neural network to estimate probability distributions rather than point-estimates (we talk more on this for the tasks of regression and classification below). In doing so, we allow our models to capture Aleatoric Uncertainty during training.

Second, they propose that at prediction time, you sample and combine predictions from multiple realizations of your neural network to get a final prediction and its uncertainty. This procedure helps our networks capture Epistemic uncertainty.

Monte Carlo Dropout

The deep learning community often uses Dropout to prevent models from overfitting. The idea is easy to implement: just randomly zero-out activations in your neural network with rate $p$ at training time and scale your activations by $p$ at test-time.

It turns out Dropout with some modifications is also useful for estimating uncertainty as described by Gal and Ghahramani. As long as your neural networks are trained with a few Dropout layers, you can use this method at prediction-time to obtain an estimate of uncertainty for your model.

The approach works by combining the predictions of several “realizations” of your neural network, which are essentially multiple forward passes of the same data point $\mathbf{x}$ through your network while applying different dropout masks $\mathbf{w}_t$ .

Unlike traditional Dropout networks, Monte Carlo Dropout (MC Dropout) networks applies dropout both at train-time and at test-time.

Algorithm:

Train a neural network $f_\theta(\mathbf{x})$ containing Dropout layers and a probabilistic loss appropriate for either your regression or classification task (see below) .
At test time, perform $T$ stochastic forward passes through $f_\theta(\mathbf{x})$ to obtain predictions for input $\mathbf{x}$ .
Depending on whether you are doing regression or classification, “combine” predictions as described below to obtain an Expectation-based prediction and uncertainty estimate.

Deep Ensembles

Another way to estimate uncertainty is by using model ensembling as described in the paper Simple and Scalable Predictive Uncertainty Estimation using Deep Ensembles.

The approach is quite similar to MC Dropout, and in fact, one way to interpret MC Dropout is to view it as a form of model ensembling.

The major difference with this approach is that rather than using a single trained network to make predictions with several randomly sampled dropout masks, we use $M$ trained models initialized from random starting points to collect our Monte Carlo samples.

Estimating uncertainty for regression

Defining the Probabilistic Loss Function: When training models for the regression task, we usually minimize the error between some target values $y$ and predicted values $\hat{y}$ using the Mean Squared Error loss.

To obtain uncertainty estimates with MC Dropout or Model Ensembling however, we must take a more probabalistic view. Rather than predicting a single scalar value $\hat{y}$ , we assume our target data is normally distributed and predict a Gaussian distribution $\mathcal{N}$ parameterized with mean $\hat{\mu}$ and variance $\hat{\sigma}^2$ .

\begin{equation} \hat{\mu}, \hat{\sigma}^2 = f_\theta(\mathbf{x}) \end{equation}

\begin{equation} p_{\theta}(y | \mathbf{x}) = \mathcal{N}(\hat{\mu}, \hat{\sigma}^2) \end{equation}

For our loss, instead of minimizing the difference to the predicted and target variable, we minimize the difference of our predictive distribution to the target distribution using the Negative Log Likelihood loss:

\begin{equation} - \log{p_{\theta}(y | \mathbf{x}}) = \frac{\log{\hat{\sigma}^2}}{2} + \frac{(y - \hat{\mu})^2}{2\hat{\sigma}^2} \end{equation}

(As an aside, I find this loss quite facinating. Notice here, we’re never explicitly providing the network an “uncertainty label” or target $\sigma^2$ . The network implicitly learns to capture the variance through the balance of the $\hat{\sigma}^2$ terms in the numerator and denominator.)

Making Predictions and Quantifying Uncertainty: Once we’ve trained our model, if we’re performing Monte Carlo Dropout, we sample dropout masks $\mathbf{w_t}$ and perform forward passes through $f_\theta(\mathbf{x; \mathbf{w_t}})$ to obtain $T$ samples:

\begin{equation} \hat{\mu}_{t}, \hat{\sigma}_{t}^2 = f_\theta(\mathbf{x; \mathbf{w_t}}) \end{equation}

With these Monte Carlo samples $\hat{\mu}_{t}$ , $\hat{\sigma}_{t}^2$ in hand, we can now compute our final regression prediction $\hat{y}_{\ast}$ and its uncertainty $\hat{\sigma}_{\ast}^{2}$ :

\begin{equation} \hat{y}_{\ast} = \frac{1}{T}\sum_{t\in{T}}{\hat{\mu}_{t}} \end{equation}

\begin{equation} \hat{\sigma}_{\ast}^{2} = \frac{1}{T}\sum_{t\in{T}}{(\hat{\sigma}_{t}^2 + \hat{\mu}_{t}^2)} - \hat{y}_{\ast}^2 \end{equation}

If we’re using Model Ensembling, rather than performing $T$ forward passes through a single network with randomly sampled $\mathbf{w}_t$ dropout masks, we instead get our predictions from $M$ trained models whose parameters $\mathbf{\theta}_m$ are initialized to random starting points. Everything else remains the same.

Note: These formulations for regression are described in follow-on papers to the MC Dropout paper from Kendall and Gal; Lakshminarayanan et. al also derives the same formulation using Proper Scoring Rules.

Estimating uncertainty for classification

Defining the Probabilistic Loss Function: The great news is that for classification, we do not need to modify the loss in order to obtain meaningful uncertainty estimates using Monte Carlo Dropout or Model Ensembling. This is because the predictions of a conventional neural network classifier uses the Softmax function which already parameterizes a discrete probability distribution.

Likewise, the Cross Entropy loss used to optimize neural network classifiers is already minimizing the the difference between our target and predictive distributions (it’s basically another name for the negative log likelihood). For these reasons, we can keep our classification network’s loss mechanics exactly the same.

Making Predictions and Quantifying Uncertainty: Once we’ve trained a standard network for classification, it is simple to obtain an expectation-based prediction and uncertainty estimate for our model.

If we are performing MC Dropout, to get a final prediction $\mathbf{\hat{y}}_\ast$ , we can average the predicted softmax probabilities over $T$ stochastic forward passes of the data $\mathbf{x}$ through our network $\mathbf{f}_{\theta}(\mathbf{x}; \mathbf{w}_t)$ by sampling random dropout mask $\mathbf{w}_t$ for each pass:

\begin{equation} \mathbf{\hat{y}}_t = \mathit{Softmax}(\mathbf{f}_{\theta}(\mathbf{x}; \mathbf{w}_t)) \end{equation}

\begin{equation} \mathbf{\hat{y}}_\ast = \frac{1}{T} \sum_{t}{\mathbf{\hat{y}}_t} \end{equation}

We measure the uncertainty of our probabilistic prediction $\mathbf{\hat{y}_\ast}$ by computing its Entropy over its vector elements $\hat{y}_{\ast,c}$ :

\begin{equation} H(\mathbf{\hat{y}_\ast}) = - \sum_c^C \hat{y}_{*,i} * {\log{\hat{y}_{\ast,c}}} \end{equation}

Sample code

We implement Tensorflow 2.0 code to perform Monte Carlo Dropout and Model Ensembling for both classification and regression in the following repository:

https://github.com/huyng/incertae

Let’s take a quick look at what the code does.

We’ll first define our model below:

from tensorflow.keras.layers import Input, Dense, Dropout
from tensorflow.keras import Sequential

model = Sequential([
    Dense(20, activation='relu'),
    Dropout(.5),
    Dense(20, activation='relu'),
    Dropout(.5),
    Dense(2, activation=None),
])

Notice, that rather than outputting a single unit, we’re outputing 2 units at the end of the network for the parameters of our estimated Gaussian distribution $\hat{\mu}$ and $\hat{\sigma}^2$ .

We’ll now define the loss for the regression task based on the equations above:

def gaussian_nll(y_true, y_pred):
    """
    Gaussian negative log likelihood

    Note: to make training more stable, we optimize
    a modified loss by having our model predict log(sigma^2)
    rather than sigma^2.
    """

    y_true = tf.reshape(y_true, [-1])
    mu = y_pred[:, 0]
    si = y_pred[:, 1]
    loss = (si + tf.math.squared_difference(y_true, mu)/tf.math.exp(si)) / 2.0
    return tf.reduce_mean(loss)

model.compile(loss=gaussian_nll, optimizer='sgd')

Finally, we’ll define our prediction function that will provide us with both an uncertainty estimate and a expecation-based prediction from our model.

import numpy as np

def predict(model, x, T=20):
    '''
    Args:
        model: The trained keras model
        x: the input tensor with shape [N, M]
        T: the number of monte carlo trials to sample
    Returns:
        y_mean: The expected value of our prediction
        y_std: The standard deviation of our prediction
    '''
    mu_arr = []
    si_arr = []

    for t in range(T):
        y_pred = model(x, training=True)
        mu = y_pred[:, 0]
        si = y_pred[:, 1]

        mu_arr.append(mu)
        si_arr.append(si)

    mu_arr = np.array(mu_arr)
    si_arr = np.array(si_arr)
    var_arr = np.exp(si_arr)

    y_mean = np.mean(mu_arr, axis=0)
    y_variance = np.mean(var_arr + mu_arr**2, axis=0) - y_mean**2
    y_std = np.sqrt(y_variance)
    return y_mean, y_std

I know it might seem odd that we’re setting train=True when using the model to predict, but this is how the Keras framework determines that it needs to sample a random dropout mask when making a forward pass.

Let’s use our function now:

y_mean, y_std = predict(model, x)

Here, y_mean is the expected value of our estimated distribution and y_std is standard deviation and can be used for our uncertainty estimate.

How good are these uncertainty estimates?

We can review the experiments in A Systematic Comparison of Bayesian Deep Learning Robustness in Diabetic Retinopathy Tasks to get a sense of how well the proposed uncertainty estimates capture the concept of uncertainty.

In this paper, the authors train a image classifier to predict whether a patient suffers from Diabetic Retinopathy based on pictures of the patient’s cornea. They train models using both techniques discussed in this blog post (in addition to a few other techniques used for estimating uncertainty).

To test whether their uncertainty estimates meaningfully capture uncertainty, they propose a simple evaluation protocol:

Refer a fixed percentage of the test dataset to a expert human oracle by sweeping a threshold over the uncertainty estimates provided by their models.
Report their model’s accuracy on the remaining retained data split (i.e. the samples that were not referred).

The idea behind this protocol is that an accurate measure of uncertainty would prioritize referring out the examples with high uncertainty, and as a result, the retained data would theoretically only contain examples that the model can predict with higher accuracy.

Here are the results of running this protocol on the Diabetic Retinopathy dataset:

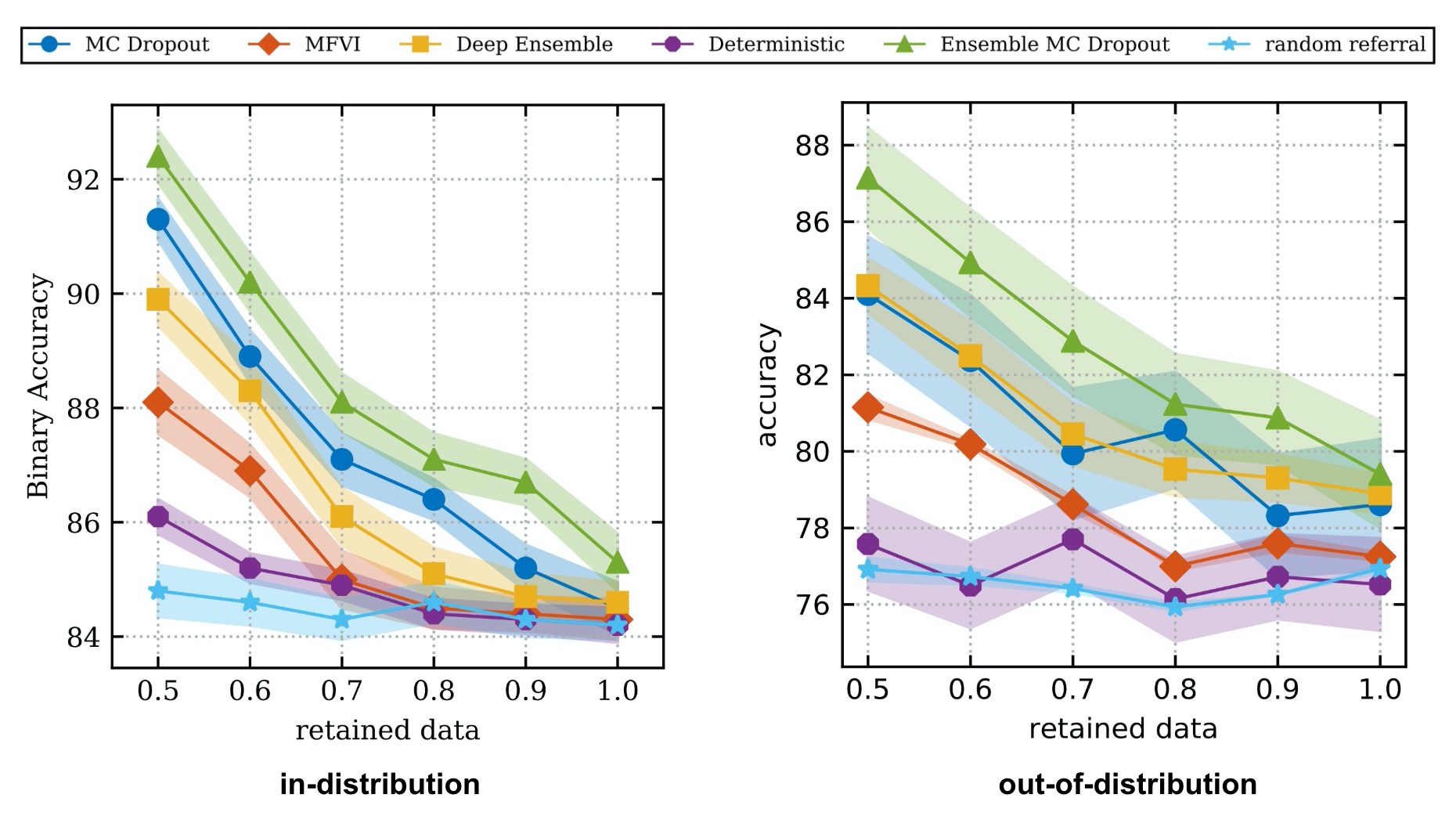
Plot of model accuracy on test data as the model refers less samples (based on the model's estimate of uncertainty) to a human oracle. For meaningful measures of uncertainty, we see accuracy increase as we decrease amount of retained data. Left: test images comes from the same machine type used for training data. Right: test images come from a different machine type than the one used for training data. [Filos et al.]

In the plot above, the authors evaluate their ability to estimate uncertainty both when the test data comes from the same distribution as the training data and when the test data comes from a different distribution.

As a sanity check we can look at the “Random Referal” baseline. Here, samples are chosen for referal at random regardless of their estimated uncertainty. As expected, randomly choosing samples neither increases nor decreases accuracy as we refer more samples to the human oracle. In contrast, both the MC Dropout and Model Ensembling methods increase accuracy as they refer more examples meaning their measures of uncertainty are finding examples that they are likely to get wrong when making a prediction.

The “Deterministic” baseline uses a single neural network to make point-estimate predictions and computes its estimate of uncertainty using entropy. In other words, it’s the conventional neural network that everyone is use to working with. It does much worse than MC Dropout and Model Ensembling for both in-distribution and out-of-distribution test sets. Interestingly for out-of-distribution data, using its uncertainty estimates is no better than random referral.

These experiments make a strong case for implementing either MC Dropout or Model ensembling to obtain more accurate uncertainty estimates. If you have the computational budget, combining both approaches (i.e. “Ensemble MC Dropout”) could yield the best results.

Moving beyond traditional leaderboard metrics

I wrote this article because in a world driven by leaderboard AUC and AP metrics, it was worth pointing out that there are other measures, specifically the quality of your model’s uncertainty estimates, that matter for production environments.

We have to know when to trust our models as much as we have to find models with the highest possible accuracy. Uncertainty quantification gives us this ability and it gives us more flexibility for deciding what to do with our model predictions.

While the article only scratches the surface of the field, hopefully you now have some basic tools to quantify uncertainty and you understand why uncertainty is so critical for developing trustworthy models.

References

Show or Add Comments